论文阅读：Multi-camera Scene Reconstruction via Graph Cuts

Vladimir Kolmogorov and Ramin Zabih

（１）介绍

文章用graph cut（图割）即能量最小化的方法，解决了多相机场景下的三维重建问题。

能量最小化方法有三个特性：

• 它把输入图像对称
• 它处理的能见度得当
• 它保持空间平滑，同时保持连续性

文章指出，传统的方法（voxel occupancy,体素占有）存在不能保证两幅图片之间的一致性的问题，并介绍了两种算法来保证图片一致性，voxel color和space carving。

（２）问题抽象

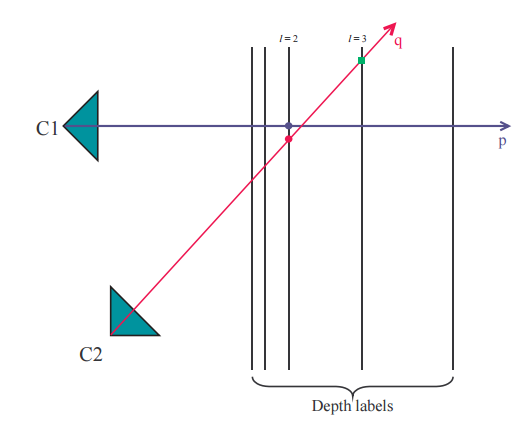
设多相机拍摄n幅图像， $ P = P_1\bigcup … \bigcup P_n $，体素$p\in P$；
令标签函数f将体素p映射到与深度相关的标签$l$;
这样3D空间中的一个点就可以用一个\对来表示。
这样的点只有当他们处于同一个label，即$l$相等时他们才有相互联系；

定义需要最小化的能量函数：
$E(f) = E{data}(f) + E{smoothness}(f) + E_{visibility}(f)$

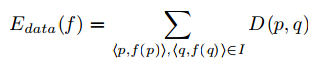
其中$D(p, q)$是体素$p$和体素$q$之间不可见的地方。

$$$$

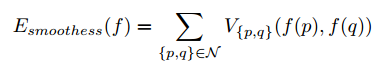
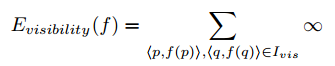
（３）图割

图割（Graph cuts）是一种十分有用和流行的能量优化算法。

此方法把图像分割问题与图额最小割（min cut）问题相关联。首先用一个无向图$G = $表示要分割的图像，$V$和$E$分别是顶点（vertex）和边（edge）的集合。此处的Graph和普通的Graph稍有不同。普通的图由顶点和边构成，如果边是有方向的则成为有向图，否则为无向图。而且边是有权值的，不同的边可以又不同的权值，分别代表不同的物理意义。而Graph Cuts涉及的图是在普通图的基础上多了２个顶点，这两个定点分别用符号”S“和”T“表示，统称为终端顶点。其它所有的顶点都必须和这２个顶点相连形成边集合中的一部分。所以Graph CUts中有两种顶点，也有两种边。

• 第一种普通顶点对应于图像中的每个像素。每两个邻域顶点（对应于图像中没两个邻域像素）的连接就是一条边。这种边也叫n-links。
• 除图像像素外，还有另外两个终端顶点，叫源点S(source)和汇点T(sink)。每个普通顶点和这两个终端顶点之间都有连接，组成第二种边，称为t-links。

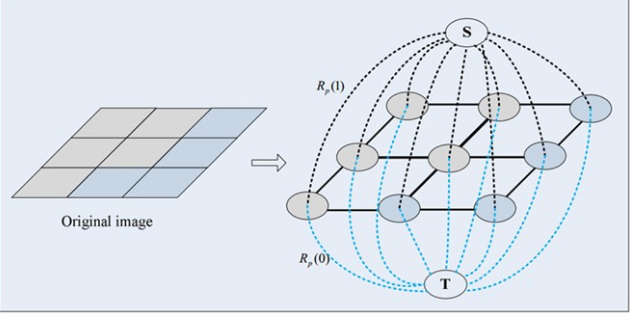
图中每条边都有一个非负的权值we，也可以理解为cost（代价或者费用）。一个cut（割）就是图中边集合E的一个子集C，那这个割的cost（表示为|C|）就是边子集C的所有边的权值的总和。

Graph Cuts中的Cuts是指这样一个边的集合，很显然这些边集合包括了上面2种边，该集合中所有边的断开会导致残留”S”和”T”图的分开，所以就称为“割”。如果一个割，它的边的所有权值之和最小，那么这个就称为最小割，也就是图割的结果。

Graph cut的3x3图像分割示意图：我们取两个种子点（就是人为的指定分别属于目标和背景的两个像素点），然后我们建立一个图，图中边的粗细表示对应权值的大小，然后找到权值和最小的边的组合，也就是（c）中的cut，即完成了图像分割的功能。